La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...

4
PM-5/1520
MEDIDOR ÓPTICO DE ALTURAS
El medidor de alturas Suunto PM-5/1520 es un instrumento que permite medir
alturas, especialmente de árboles, con una gran exactitud y agilidad. La carcasa del
instrumento es de una aleación de aluminio anodizado resistente a la corrosión. La
escala se mueve sobre un rodamiento especial dentro de un contenedor de plástico
sellado herméticamente y lleno de un líquido que garantiza que se puede mover
libremente y detenerse en poco tiempo. El líquido es anticongelante, conserva todas
sus propiedades de amortiguación en condiciones de trabajo y elimina las irritantes
vibraciones de la escala.
INSTRUCCIONES DE USO
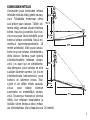
Al medir desde las distancias de 15 y 20 m, las alturas de los árboles pueden leerse
directamente en las escalas del instrumento. Las lecturas obtenidas deben
multiplicarse por dos si la lectura se realiza desde distancias de 30 m y 40 m. El
medidor de alturas Suunto también puede usarse para determinar el ángulo de una
pendiente. Esto se realiza haciendo una lectura a lo largo de la línea de una
pendiente con la escala de 20 m del lado izquierdo del instrumento. La lectura
obtenida puede buscarse en la tabla de conversión de la parte trasera del
instrumento para obtener el ángulo.

5
MEDICIÓN DE ALTURAS
La medición de la altura del árbol
debe realizarse desde la distancia
medida, de la forma siguiente: el
observador mira la copa del árbol con
los dos ojos abiertos. El objeto
observado, el retículo y la escala se
ven a la vez en el campo de visión del
instrumento. Tan pronto como el
retículo coincide con la copa del árbol,
puede leerse la altura del árbol (en
este ejemplo con la escala de 20 m
situada a la izquierda del
instrumento). La lectura obtenida es la
altura del árbol medida desde la altura
de los ojos del observador. Aún falta
medir la base del árbol. Si ésta se
encuentra por debajo de la altura de
los ojos del observador, la altura real
del árbol se obtiene sumando las dos
lecturas. Si se encuentra por encima
de la altura de los ojos del
observador, la altura del árbol se
obtiene obteniendo la diferencia de
las dos lecturas. De hecho, en el segundo caso la distancia no puede medirse
horizontalmente. Por tanto, para obtener un resultado exactamente correcto debe

6
seguir los pasos indicados a continuación. En un terreno llano, suele bastar con leer
la altura de las copas: sólo es necesario añadir la altura de los ojos del observador
(1.60 m en este caso), que es un dato conocido.
INSTRUCCIONES DE USO DEL
NOMOGRAMA
Si no es posible determinar la distancia
desde la horizontal como se indicaba
anteriormente, debido a que el terreno está
muy inclinado, se debe utilizar el
nomograma de la página 7.
CÓMO DETERMINAR LA DISTANCIA BÁSICA
Dado que este instrumento no incorpora ningún prisma, la distancia básica (por
ejemplo 15 m) debe determinarse con una medición con cinta métrica sobre el
terreno. Mida la altura de la copa y de la base y súmelas o réstelas para obtener la
altura aparente. En el nomograma de la página 7, busque la altura aparente en la
escala del lado derecho. En la escala doble de la izquierda, busque el valor obtenido
al medir la base del árbol. Observe que las lecturas para las pendientes ascendentes
y las descendentes deben hacerse desde lados distintos de la escala. Conecte estos
dos puntos del nomograma con una línea recta. La escala central del nomograma
indica ahora la altura real del árbol.

7
Aviso importante
Los ejes de los ojos de algunas personas
no son paralelos. Esto se conoce como
heteroforia. Esta situación puede incluso
variar con el tiempo y depender de otros
factores diferentes. Por tanto, para
asegurarse de que este fenómeno no
afecte a la exactitud de las lecturas, se
recomienda que el usuario compruebe si
presenta esta tendencia antes de
empezar a realizar las lecturas. Esto se
hace como sigue: Tome una lectura con
los dos ojos abiertos y cierre a
continuación el ojo libre. Si la lectura no
cambia apreciablemente, quiere decir que
no existen problemas de alineación de los
ejes del ojo y puede mantener los dos
ojos abiertos. Si detecta una diferencia en
las lecturas, mantenga el otro ojo cerrado
y mire a media altura a un lado de la
carcasa del instrumento. Esto creará una
ilusión óptica que hace que el retículo
continúe más allá de la carcasa del
instrumento y se vea superpuesto sobre el
objeto.
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
2
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
m
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
m
L-20
m
Lectura desde la base
Altura corregida
Altura aparente
Pendiente
descendente
Pendiente
ascendente

8
PM-5
INCLINÓMETRO PARA LECTURA ÓPTICA
Su resistente diseño de bolsillo hace que el
INCLINÓMETRO SUUNTO sea idóneo para todo tipo
de trabajos. Su diseño permite una lectura rápida y
sencilla a través de un visor sin paralaje.
La observación y la lectura de la escala se hacen
simultáneamente. No requiere girar ningún mando,
centrar ninguna burbuja ni realizar ajuste alguno.
En las situaciones con poco espacio disponible, como
en los trabajos geológicos y mineralógicos, la
inclinación de los estratos y otras formaciones puede
medirse situando el instrumento a lo largo del contorno
de la superficie de la formación y leyendo el ángulo
directamente a través de la ventana lateral.
Características constructivas
La carcasa es de aluminio ligero resistente a la
corrosión.
La escala se apoya en un conjunto de rodamiento de
piedra preciosa y todas las partes móviles están
sumergidas en un líquido amortiguador, dentro de un contenedor de plástico sellado
herméticamente y de alta resistencia. El líquido amortigua todas las vibraciones no
deseadas en la escala y permite que ésta se mueva con suavidad y sin sacudidas.
El material del contenedor no se altera con la luz solar ni el contacto con el agua. El
líquido es anticongelante y no se congela en el ártico ni se evapora en los trópicos.
Escalas en
pies + y –
Escalas en
grados + y –
Retículo
ampliado por
ilusión óptica
Escala de grados
adicional en
ventana lateral

9
Especificaciones
Peso: 120 g / 4,2 onzas. Dimensiones: 74 x 52 x 15 mm / 2 3/4 x 2 x 5/8 pulg. Las
escalas ópticas están graduadas en grados, de 0° a ±90° y del 0% al ±150%.
La parte trasera del instrumento tiene impresa una tabla de cosenos.
Resolución
Permite leer directamente con una exactitud de un grado o un 1%. Permite obtener
estimaciones de 10 minutos o 1/5 de 1%, en este último caso aplicando naturalmente
las lecturas cercanas al nivel cero.
VERSIONES DE PM-5 DISPONIBLES
El PM-5/360 PC básico ha sido modificado para incorporar distintas combinaciones
de escalas para usos especiales. Por tanto, existe una versión con una escala de
”grados nuevos” o grados centesimales. En este caso, en lugar de la división normal
de 360 grados, el círculo completo se divide en 400 grados centesimales (g). La
escala de porcentaje que tiene asociada es una escala normal. Este modelo es el
PM-5/400 PC.

10
INSTRUCCIONES DE USO
Las lecturas se suelen tomar con el ojo derecho. Debido a las diferencias existentes
en la agudeza visual de cada ojo y en función de sus preferencias personales, en
ocasiones resulta más fácil usar el ojo izquierdo. Es de una importancia capital
mantener los dos ojos abiertos. La mano con la que sujete el instrumento no debe
obstaculizar la visión del otro ojo.
El instrumento se sostiene delante del ojo con el que se realiza la medición, de forma
que sea posible leer la escala a través del ocular y la ventana lateral redonda quede
orientada hacia la izquierda. Para apuntar el instrumento hacia el objeto, eleve o baje
el instrumento hasta que el retículo se vea superpuesto sobre el punto a medir. Al
mismo tiempo, la posición del retículo sobre la escala indica la medida. Debido a una
ilusión óptica, el retículo (la cruz de hilos) parece continuar más allá de la carcasa y
por tanto puede observarse fácilmente superpuesto sobre el terreno o el objeto.
La escala izquierda indica el ángulo de pendiente en grados, respecto del plano
horizontal a la altura de los ojos. La escala derecha indica la altura del punto
visualizado respecto de la misma horizontal a la altura de los ojos y se expresa en
porcentaje de la distancia horizontal. En el ejemplo siguiente se ilustra este
procedimiento:

11
La tarea consiste en medir la
altura de un árbol a una
distancia de 25 m/82 pies
sobre terreno llano. Se inclina
el instrumento de forma que el
retículo se vea superpuesto
sobre la copa (el ápice) del
árbol. La lectura obtenida será
del 48 por ciento
(aproximadamente 25,5°).
Dado que la distancia es de
25 m/82 pies, la altura del árbol
es de 48 / 100 x 25 m = aprox.
12 m o de forma equivalente 48
/ 100 x 25 m = aprox. 12 m o de
forma equivalente 48 / 100 x 82
pies = aprox. 39 pies. A esta
cifra debe sumársele la altura
de los ojos’ desde el suelo, por
ejemplo 1,6 m ó 5½ pies. La
suma es 13,6 m ó 44½ pies, la
altura del árbol.
En mediciones muy exactas, y especialmente en terrenos inclinados, se toman dos
medidas, una hasta el extremo superior del tronco y otra hasta su base. Si la base
del tronco se encuentra por debajo de la altura de los ojos, se obtienen y suman los
porcentajes. La altura total es la suma de porcentajes de la distancia horizontal. Por

12
ejemplo, si la lectura del ápice del 41% y la lectura del suelo es del 13%, la altura
total del árbol medida desde una distancia de 25 m / 82 pies es de (41 + 13) / 100 x
25 m = 54 / 100 x 25 m = aprox. 13,5 m o de forma equivalente en pies (41 + 13) /
100 x 82 pies = 54 / 100 x 82 pies = aprox. 44½ pies.
Si la base del tronco se encuentra por encima del nivel de los ojos, la lectura de la
base se resta de la lectura del ápice y la altura total es la diferencia de porcentajes de
la distancia horizontal.
Por ejemplo, si la lectura del ápice indica un 65% y la lectura de la base indica 14%,
la altura total es de (64 – 14) / 100 x 25 m = 50 / 100 x 25 m = 12,5 m o de forma
equivalente en pies (64 – 14) / 100 x 82 pies = 50 / 100 x 82 pies = 41 pies. Si hace
los cálculos mentalmente, es recomendable tomar las mediciones a distancias de 50,
100 ó 200 metros o pies para que resulte más sencillo.

13
Todas las lecturas de la escala de porcentajes se basan en la distancia horizontal.
Esto significa que si se mide la distancia en un terreno inclinado a lo largo del
terreno, se introduce un error que es necesario corregir para conseguir resultados
exactos. El error no es significativo para la mayoría de los fines si el terreno presenta
una inclinación reducida, pero aumenta progresivamente con el aumento de la
inclinación.
La relación trigonométrica es la siguiente:
H = h x cos
α
Donde H es la altura real o corregida, h es la altura observada y α (alfa) es el ángulo
de la pendiente del terreno. Con la ayuda de la ecuación anterior, la corrección
también puede hacerse en la distancia. En este caso, h equivale a la distancia
medida sobre el terreno y H es la distancia horizontal a calcular. Si se usa la distancia
corregida, no se requiere ninguna corrección en la altura observada. Al calcular la
distancia horizontal a partir de la distancia sobre el terreno y la inclinación, es
necesario tener en cuenta que se introduce un error si la pendiente se mide desde la
altura de los ojos hasta la base del tronco. La medición de la inclinación a lo largo del
terreno sería trabajosa e incómoda. Sin embargo, no se introduce ningún error si el
ángulo de inclinación se mide desde la altura de los ojos hasta una marca de
observación realizada o situada en al superficie del tronco a la altura de los ojos,
dado que las dos líneas de medición quedan paralelas. El ángulo de inclinación real
es de 9 grados.

14
El ejemplo mostrado en la figura
siguiente ilustra los dos métodos
de cálculo.
Método 1. Mida la distancia a
nivel del terreno. Se determina
que es de 25 m / 82 pies. A
continuación, mida el ángulo de
inclinación. Es de 9 grados. Lea
los porcentajes del punto
superior y del terreno. Se trata
del 29% y el 23%.
Calcule:
Obtenga el 52 por ciento de 25 m/82 pies. Es 13 m/42,6 pies. Multiplique este valor
por el coseno de 9 grados.
0,987 x 13 m = 12,8 m, o de forma equivalente en pies, 0,987 x 42,6 pies = 42 pies.
Método 2. Multiplique la distancia sobre el terreno por el coseno del ángulo de
inclinación.
0,987 x 25 m = 24,6 m, o de forma equivalente en pies, 0,987 x 82 pies = 80,9 pies.
23
100
-------- -
29
100
-------- -
52
100
-------- -=+

15
Sume los porcentajes leídos de la forma indicada arriba y calcule la distancia
corregida con la suma de los porcentajes.
O de forma equivalente en pies
En este ejemplo se muestra que un ángulo de inclinación de 9 grados causa una
corrección de sólo un 2,3 por ciento, pero si el ángulo de inclinación es de 35 grados,
la corrección supone la reducción de la altura observada en aproximadamente un 18
por ciento.
52
100
-------- -
24 6m 12 8m,=,×
52
100
-------- -
80 9ft 42ft=,×

16
CORRECCIÓN DE ALTURA CON EL NOMOGRAMA
Si se utiliza el nomograma, se elimina la necesidad de realizar cálculos de
corrección. Sólo se requiere una regla u otro objeto fácil de usar con un borde recto,
para obtener la solución nomográfica. Para usar el nomograma, coloque la regla de
forma que su borde corte la escala de ángulos de la izquierda en el punto que
corresponda al ángulo de inclinación y la escala de altura observada (a la derecha)
en el punto pertinente. La altura (o distancia) corregida se lee en el punto en el que el
borde corta la escala de altura de la parte central. Si se utiliza una distancia de
medición de 100 m / 100 pies sobre el terreno, el procedimiento de corrección es
muy sencillo. En este caso no se requiere ninguna medición del ángulo de
inclinación. Sólo es necesario hacer la lectura del punto superior y la del punto a la
altura del terreno. En función de la situación, su suma o resta indica la altura
aparente, directamente en pies. A continuación, este valor se corrige de la forma
siguiente: En primer lugar, busque en la escala derecha del nomograma el punto
correspondiente a la altura aparente. En segundo lugar, busque en la escala doble
de la izquierda el punto que indica la lectura del punto situado a la altura del terreno.
En tercer lugar, conecte estos puntos. La lectura corregida se indica en la escala
central pertinente, en el punto de intersección. En este procedimiento, el ángulo de
inclinación puede omitirse, dado que la escala de puntos izquierda para el terreno se
ha creado de forma que se tengan en cuenta el ángulo de inclinación y la altura
media de los ojos, de 1,6 m/5,5 pies.
CUBIERTA DE CARCASA DE INSTRUMENTO SUUNTO KB-14 Y PM-5
La cubierta de carcasa de instrumento es adecuada para los modelos KB y PM
siguientes: KB-14 (todos los modelos) y PM-5.
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
La página se está cargando...
Transcripción de documentos
PM-5/1520 MEDIDOR ÓPTICO DE ALTURAS El medidor de alturas Suunto PM-5/1520 es un instrumento que permite medir alturas, especialmente de árboles, con una gran exactitud y agilidad. La carcasa del instrumento es de una aleación de aluminio anodizado resistente a la corrosión. La escala se mueve sobre un rodamiento especial dentro de un contenedor de plástico sellado herméticamente y lleno de un líquido que garantiza que se puede mover libremente y detenerse en poco tiempo. El líquido es anticongelante, conserva todas sus propiedades de amortiguación en condiciones de trabajo y elimina las irritantes vibraciones de la escala. INSTRUCCIONES DE USO Al medir desde las distancias de 15 y 20 m, las alturas de los árboles pueden leerse directamente en las escalas del instrumento. Las lecturas obtenidas deben multiplicarse por dos si la lectura se realiza desde distancias de 30 m y 40 m. El medidor de alturas Suunto también puede usarse para determinar el ángulo de una pendiente. Esto se realiza haciendo una lectura a lo largo de la línea de una pendiente con la escala de 20 m del lado izquierdo del instrumento. La lectura obtenida puede buscarse en la tabla de conversión de la parte trasera del instrumento para obtener el ángulo. 4 MEDICIÓN DE ALTURAS La medición de la altura del árbol debe realizarse desde la distancia medida, de la forma siguiente: el observador mira la copa del árbol con los dos ojos abiertos. El objeto observado, el retículo y la escala se ven a la vez en el campo de visión del instrumento. Tan pronto como el retículo coincide con la copa del árbol, puede leerse la altura del árbol (en este ejemplo con la escala de 20 m situada a la izquierda del instrumento). La lectura obtenida es la altura del árbol medida desde la altura de los ojos del observador. Aún falta medir la base del árbol. Si ésta se encuentra por debajo de la altura de los ojos del observador, la altura real del árbol se obtiene sumando las dos lecturas. Si se encuentra por encima de la altura de los ojos del observador, la altura del árbol se obtiene obteniendo la diferencia de las dos lecturas. De hecho, en el segundo caso la distancia no puede medirse horizontalmente. Por tanto, para obtener un resultado exactamente correcto debe 5 seguir los pasos indicados a continuación. En un terreno llano, suele bastar con leer la altura de las copas: sólo es necesario añadir la altura de los ojos del observador (1.60 m en este caso), que es un dato conocido. INSTRUCCIONES DE USO DEL NOMOGRAMA Si no es posible determinar la distancia desde la horizontal como se indicaba anteriormente, debido a que el terreno está muy inclinado, se debe utilizar el nomograma de la página 7. CÓMO DETERMINAR LA DISTANCIA BÁSICA Dado que este instrumento no incorpora ningún prisma, la distancia básica (por ejemplo 15 m) debe determinarse con una medición con cinta métrica sobre el terreno. Mida la altura de la copa y de la base y súmelas o réstelas para obtener la altura aparente. En el nomograma de la página 7, busque la altura aparente en la escala del lado derecho. En la escala doble de la izquierda, busque el valor obtenido al medir la base del árbol. Observe que las lecturas para las pendientes ascendentes y las descendentes deben hacerse desde lados distintos de la escala. Conecte estos dos puntos del nomograma con una línea recta. La escala central del nomograma indica ahora la altura real del árbol. 6 Aviso importante Los ejes de los ojos de algunas personas no son paralelos. Esto se conoce como heteroforia. Esta situación puede incluso variar con el tiempo y depender de otros factores diferentes. Por tanto, para asegurarse de que este fenómeno no afecte a la exactitud de las lecturas, se recomienda que el usuario compruebe si presenta esta tendencia antes de empezar a realizar las lecturas. Esto se hace como sigue: Tome una lectura con los dos ojos abiertos y cierre a continuación el ojo libre. Si la lectura no cambia apreciablemente, quiere decir que no existen problemas de alineación de los ejes del ojo y puede mantener los dos ojos abiertos. Si detecta una diferencia en las lecturas, mantenga el otro ojo cerrado y mire a media altura a un lado de la carcasa del instrumento. Esto creará una ilusión óptica que hace que el retículo continúe más allá de la carcasa del instrumento y se vea superpuesto sobre el objeto. L-20 Pendiente descendente 2 4 5 6 m m 20 20 19 18 19 3 17 18 4 16 m 0 1 2 7 8 5 Pendiente ascendente 9 10 11 12 13 15 14 6 7 8 17 16 13 12 11 15 14 10 13 9 12 9 14 10 8 15 11 11 7 16 17 18 10 12 6 9 13 5 19 8 14 20 15 21 4 Altura corregida 7 16 6 Lectura desde la base Altura aparente 7 PM-5 Escalas en pies + y – INCLINÓMETRO PARA LECTURA ÓPTICA Su resistente diseño de bolsillo hace que el INCLINÓMETRO SUUNTO sea idóneo para todo tipo de trabajos. Su diseño permite una lectura rápida y Escalas en sencilla a través de un visor sin paralaje. grados + y – La observación y la lectura de la escala se hacen simultáneamente. No requiere girar ningún mando, centrar ninguna burbuja ni realizar ajuste alguno. En las situaciones con poco espacio disponible, como Retículo por en los trabajos geológicos y mineralógicos, la ampliado ilusión óptica inclinación de los estratos y otras formaciones puede medirse situando el instrumento a lo largo del contorno Escala de grados de la superficie de la formación y leyendo el ángulo adicional en ventana lateral directamente a través de la ventana lateral. Características constructivas La carcasa es de aluminio ligero resistente a la corrosión. La escala se apoya en un conjunto de rodamiento de piedra preciosa y todas las partes móviles están sumergidas en un líquido amortiguador, dentro de un contenedor de plástico sellado herméticamente y de alta resistencia. El líquido amortigua todas las vibraciones no deseadas en la escala y permite que ésta se mueva con suavidad y sin sacudidas. El material del contenedor no se altera con la luz solar ni el contacto con el agua. El líquido es anticongelante y no se congela en el ártico ni se evapora en los trópicos. 8 Especificaciones Peso: 120 g / 4,2 onzas. Dimensiones: 74 x 52 x 15 mm / 2 3/4 x 2 x 5/8 pulg. Las escalas ópticas están graduadas en grados, de 0° a ±90° y del 0% al ±150%. La parte trasera del instrumento tiene impresa una tabla de cosenos. Resolución Permite leer directamente con una exactitud de un grado o un 1%. Permite obtener estimaciones de 10 minutos o 1/5 de 1%, en este último caso aplicando naturalmente las lecturas cercanas al nivel cero. VERSIONES DE PM-5 DISPONIBLES El PM-5/360 PC básico ha sido modificado para incorporar distintas combinaciones de escalas para usos especiales. Por tanto, existe una versión con una escala de ”grados nuevos” o grados centesimales. En este caso, en lugar de la división normal de 360 grados, el círculo completo se divide en 400 grados centesimales (g). La escala de porcentaje que tiene asociada es una escala normal. Este modelo es el PM-5/400 PC. 9 INSTRUCCIONES DE USO Las lecturas se suelen tomar con el ojo derecho. Debido a las diferencias existentes en la agudeza visual de cada ojo y en función de sus preferencias personales, en ocasiones resulta más fácil usar el ojo izquierdo. Es de una importancia capital mantener los dos ojos abiertos. La mano con la que sujete el instrumento no debe obstaculizar la visión del otro ojo. El instrumento se sostiene delante del ojo con el que se realiza la medición, de forma que sea posible leer la escala a través del ocular y la ventana lateral redonda quede orientada hacia la izquierda. Para apuntar el instrumento hacia el objeto, eleve o baje el instrumento hasta que el retículo se vea superpuesto sobre el punto a medir. Al mismo tiempo, la posición del retículo sobre la escala indica la medida. Debido a una ilusión óptica, el retículo (la cruz de hilos) parece continuar más allá de la carcasa y por tanto puede observarse fácilmente superpuesto sobre el terreno o el objeto. La escala izquierda indica el ángulo de pendiente en grados, respecto del plano horizontal a la altura de los ojos. La escala derecha indica la altura del punto visualizado respecto de la misma horizontal a la altura de los ojos y se expresa en porcentaje de la distancia horizontal. En el ejemplo siguiente se ilustra este procedimiento: 10 La tarea consiste en medir la altura de un árbol a una distancia de 25 m/82 pies sobre terreno llano. Se inclina el instrumento de forma que el retículo se vea superpuesto sobre la copa (el ápice) del árbol. La lectura obtenida será del 48 por ciento (aproximadamente 25,5°). Dado que la distancia es de 25 m/82 pies, la altura del árbol es de 48 / 100 x 25 m = aprox. 12 m o de forma equivalente 48 / 100 x 25 m = aprox. 12 m o de forma equivalente 48 / 100 x 82 pies = aprox. 39 pies. A esta cifra debe sumársele la altura de los ojos’ desde el suelo, por ejemplo 1,6 m ó 5½ pies. La suma es 13,6 m ó 44½ pies, la altura del árbol. En mediciones muy exactas, y especialmente en terrenos inclinados, se toman dos medidas, una hasta el extremo superior del tronco y otra hasta su base. Si la base del tronco se encuentra por debajo de la altura de los ojos, se obtienen y suman los porcentajes. La altura total es la suma de porcentajes de la distancia horizontal. Por 11 ejemplo, si la lectura del ápice del 41% y la lectura del suelo es del 13%, la altura total del árbol medida desde una distancia de 25 m / 82 pies es de (41 + 13) / 100 x 25 m = 54 / 100 x 25 m = aprox. 13,5 m o de forma equivalente en pies (41 + 13) / 100 x 82 pies = 54 / 100 x 82 pies = aprox. 44½ pies. Si la base del tronco se encuentra por encima del nivel de los ojos, la lectura de la base se resta de la lectura del ápice y la altura total es la diferencia de porcentajes de la distancia horizontal. Por ejemplo, si la lectura del ápice indica un 65% y la lectura de la base indica 14%, la altura total es de (64 – 14) / 100 x 25 m = 50 / 100 x 25 m = 12,5 m o de forma equivalente en pies (64 – 14) / 100 x 82 pies = 50 / 100 x 82 pies = 41 pies. Si hace los cálculos mentalmente, es recomendable tomar las mediciones a distancias de 50, 100 ó 200 metros o pies para que resulte más sencillo. 12 Todas las lecturas de la escala de porcentajes se basan en la distancia horizontal. Esto significa que si se mide la distancia en un terreno inclinado a lo largo del terreno, se introduce un error que es necesario corregir para conseguir resultados exactos. El error no es significativo para la mayoría de los fines si el terreno presenta una inclinación reducida, pero aumenta progresivamente con el aumento de la inclinación. La relación trigonométrica es la siguiente: H = h x cos α Donde H es la altura real o corregida, h es la altura observada y α (alfa) es el ángulo de la pendiente del terreno. Con la ayuda de la ecuación anterior, la corrección también puede hacerse en la distancia. En este caso, h equivale a la distancia medida sobre el terreno y H es la distancia horizontal a calcular. Si se usa la distancia corregida, no se requiere ninguna corrección en la altura observada. Al calcular la distancia horizontal a partir de la distancia sobre el terreno y la inclinación, es necesario tener en cuenta que se introduce un error si la pendiente se mide desde la altura de los ojos hasta la base del tronco. La medición de la inclinación a lo largo del terreno sería trabajosa e incómoda. Sin embargo, no se introduce ningún error si el ángulo de inclinación se mide desde la altura de los ojos hasta una marca de observación realizada o situada en al superficie del tronco a la altura de los ojos, dado que las dos líneas de medición quedan paralelas. El ángulo de inclinación real es de 9 grados. 13 El ejemplo mostrado en la figura siguiente ilustra los dos métodos de cálculo. Método 1. Mida la distancia a nivel del terreno. Se determina que es de 25 m / 82 pies. A continuación, mida el ángulo de inclinación. Es de 9 grados. Lea los porcentajes del punto superior y del terreno. Se trata del 29% y el 23%. Calcule: 29- 52 23- + --------------= --------100 100 100 Obtenga el 52 por ciento de 25 m/82 pies. Es 13 m/42,6 pies. Multiplique este valor por el coseno de 9 grados. 0,987 x 13 m = 12,8 m, o de forma equivalente en pies, 0,987 x 42,6 pies = 42 pies. Método 2. Multiplique la distancia sobre el terreno por el coseno del ángulo de inclinación. 0,987 x 25 m = 24,6 m, o de forma equivalente en pies, 0,987 x 82 pies = 80,9 pies. 14 Sume los porcentajes leídos de la forma indicada arriba y calcule la distancia corregida con la suma de los porcentajes. 52-------× 24 ,6m = 12 ,8m 100 O de forma equivalente en pies 52-------× 80 ,9ft = 42ft 100 En este ejemplo se muestra que un ángulo de inclinación de 9 grados causa una corrección de sólo un 2,3 por ciento, pero si el ángulo de inclinación es de 35 grados, la corrección supone la reducción de la altura observada en aproximadamente un 18 por ciento. 15 CORRECCIÓN DE ALTURA CON EL NOMOGRAMA Si se utiliza el nomograma, se elimina la necesidad de realizar cálculos de corrección. Sólo se requiere una regla u otro objeto fácil de usar con un borde recto, para obtener la solución nomográfica. Para usar el nomograma, coloque la regla de forma que su borde corte la escala de ángulos de la izquierda en el punto que corresponda al ángulo de inclinación y la escala de altura observada (a la derecha) en el punto pertinente. La altura (o distancia) corregida se lee en el punto en el que el borde corta la escala de altura de la parte central. Si se utiliza una distancia de medición de 100 m / 100 pies sobre el terreno, el procedimiento de corrección es muy sencillo. En este caso no se requiere ninguna medición del ángulo de inclinación. Sólo es necesario hacer la lectura del punto superior y la del punto a la altura del terreno. En función de la situación, su suma o resta indica la altura aparente, directamente en pies. A continuación, este valor se corrige de la forma siguiente: En primer lugar, busque en la escala derecha del nomograma el punto correspondiente a la altura aparente. En segundo lugar, busque en la escala doble de la izquierda el punto que indica la lectura del punto situado a la altura del terreno. En tercer lugar, conecte estos puntos. La lectura corregida se indica en la escala central pertinente, en el punto de intersección. En este procedimiento, el ángulo de inclinación puede omitirse, dado que la escala de puntos izquierda para el terreno se ha creado de forma que se tengan en cuenta el ángulo de inclinación y la altura media de los ojos, de 1,6 m/5,5 pies. CUBIERTA DE CARCASA DE INSTRUMENTO SUUNTO KB-14 Y PM-5 La cubierta de carcasa de instrumento es adecuada para los modelos KB y PM siguientes: KB-14 (todos los modelos) y PM-5. 16-
 1
1
-
 2
2
-
 3
3
-
 4
4
-
 5
5
-
 6
6
-
 7
7
-
 8
8
-
 9
9
-
 10
10
-
 11
11
-
 12
12
-
 13
13
-
 14
14
-
 15
15
-
 16
16
-
 17
17
-
 18
18
-
 19
19
-
 20
20
-
 21
21
-
 22
22
-
 23
23
-
 24
24
-
 25
25
-
 26
26
-
 27
27
-
 28
28
-
 29
29
-
 30
30
-
 31
31
-
 32
32
-
 33
33
-
 34
34
-
 35
35
-
 36
36
-
 37
37
-
 38
38
-
 39
39
-
 40
40
-
 41
41
-
 42
42
-
 43
43
-
 44
44
-
 45
45
-
 46
46
-
 47
47
-
 48
48
-
 49
49
-
 50
50
-
 51
51
-
 52
52
-
 53
53
-
 54
54
-
 55
55
-
 56
56
-
 57
57
-
 58
58
-
 59
59
-
 60
60
-
 61
61
-
 62
62
-
 63
63
-
 64
64
-
 65
65
-
 66
66
-
 67
67
-
 68
68
-
 69
69
-
 70
70
-
 71
71
-
 72
72
-
 73
73
-
 74
74
-
 75
75
-
 76
76
-
 77
77
-
 78
78
-
 79
79
-
 80
80
-
 81
81
-
 82
82
-
 83
83
-
 84
84
-
 85
85
-
 86
86
-
 87
87
-
 88
88
-
 89
89
-
 90
90
-
 91
91
-
 92
92
-
 93
93
-
 94
94
-
 95
95
-
 96
96
-
 97
97
-
 98
98
-
 99
99
-
 100
100
-
 101
101
-
 102
102
-
 103
103
-
 104
104
-
 105
105
-
 106
106
-
 107
107
-
 108
108
Suunto 1520 Manual de usuario
- Categoría
- Medición
- Tipo
- Manual de usuario
en otros idiomas
- français: Suunto 1520 Manuel utilisateur
- italiano: Suunto 1520 Manuale utente
- English: Suunto 1520 User manual
- Deutsch: Suunto 1520 Benutzerhandbuch
- svenska: Suunto 1520 Användarmanual
- suomi: Suunto 1520 Ohjekirja
Artículos relacionados
Otros documentos
-
Bushnell 280750 Manual de usuario
-
DeWalt DW090K Manual de usuario
-
Celestron Oceana 71189-A Manual de usuario
-
Praktica Marine Manual de usuario
-
Celestron Oceana 71189-B Manual de usuario
-
Bosch GOL 26CK Manual de usuario
-
Quick RDS 1520 Manual de usuario
-
Celestron Cavalry 71426 Manual de usuario
-
Leica GHM007 El manual del propietario











































































































